Autor: Rudolf Pleier

In der vorliegenden Arbeit werden im ersten Kapitel Methoden entwickelt, mit denen Bedingungen an die komplexwertigen Koeffizienten der linearen Differentialgleichung gewonnen werden können, die hinreichend für das Nichtauftreten gewisser Nullstellenkonfigurationen bei den Lösungen und deren Ableitungen sind. Im zweiten Kapitel wird für reellwertige Koeffizienten das Raumpaar aus den Lösungsräumen der Differentialgleichung (L) und der dazu adjungierten Differentialgleichung (L+) mit einem skalaren Produkt B ausgestattet und damit ein duales Raumpaar erhalten. Es können allgemeine Wechselbeziehungen zwischen den Nullstellenverteilungen der Lösungen von (L) und (L+) hergeleitet werden hinsichtlich Oszillation, Existenz von nichtoszillatorischen, schwach oszillatorischen und stark oszillatorischen zweidimensionalen Unterräumen, Charakterisierungen von speziellen Doppelkegelstrukturen der Menge der nichtoszillatorischen Lösungen durch asymptotische Eigenschaften der Lösungen, Diskonjugiertheit an den Intervallgrenzen und der lokalen Diskonjugiertheit. Außerdem werden anstelle der Verwendung spezieller Koeffizientenbedingungen nun Klassen von Differentialgleichungen durch den Ausschluss gewisser Nullstellenkonfigurationen bei bestimmten Standardlösungen definiert und Wechselbeziehungen zwischen den Klassen von (L) und (L+) dargestellt. 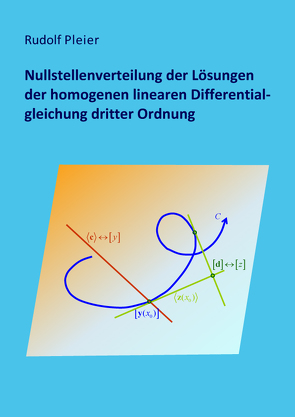Im dritten Kapitel wird die schon 1905 von Wilczynski und 1911 von Birkhoff verwendete Integralkurve C in der projektiven Ebene dargestellt, die man erhält, wenn man die Funktionswerte eines beliebig fixierten Fundamentalsystems von (L) als die homogenen Koordinaten eines Punktes in der projektiven Ebene interpretiert. Damit können die Nullstellen einer Lösung von (L) durch die Treffpunkte einer Geraden mit der Integralkurve und die Nullstellen einer Lösung von (L+) durch die Tangenten eines Punktes an die Integralkurve veranschaulicht werden. Allgemeiner wird gezeigt, dass eine bestimmte Gerade durch einen bestimmten Punkt genau dann geht, wenn die zugehörigen Lösungen von (L) und (L+) bezüglich des skalaren Produkts B orthogonal sind. Es werden verschiedene Klassen der Differentialgleichungen mittels der besonderen Gestalt der Integralkurve C veranschaulicht und umgekehrt geometrische Eigenschaften von C mittels spezieller Lösungen analytisch charakterisiert. In Verallgemeinerung eines von Birkhoff geometrisch begründeten Trennungssatzes für die Nullstellen von Lösungen werden weitere Sätze über die Nullstellenanzahl von orthogonalen bzw. nicht orthogonalen Lösungen analytisch bewiesen. Im vierten Kapitel werden Eigenschaften der Klassen KI und KII aufgezeigt hinsichtlich Charakterisierungen der Diskonjugiertheit, Charakterisierung der nichtoszillatorischen Lösungen als die nullstellenfreien Lösungen, Existenz von nichtnegativen nichttrivialen Lösungen, Existenz von stark oszillatorischen zweidimensionalen Unterräumen, Oszillation von (L) und (L+), Diskonjugiertheit an den Intervallgrenzen und Existenz von nullstellenfreien Lösungen. Ferner wird die von Birkhoff geometrisch begründete Charakterisierung der Klasse KI U KII, bei der die Tangenten von C das vorhergehende bzw. das nachfolgende Kurvenstück nicht schneiden, durch die Spiralform der Integralkurve C hier analytisch bewiesen. In diesem Zusammenhang werden einige Hilfssätze bereitgestellt und auch neue Erkenntnisse über die durch die ersten konjugierten Punkte gegebene Funktion η hergeleitet.